Algebraic topology is a field in mathematics that attempts to determine when spaces have different shapes. Let us break down what that means.
For our purposes, a space can just be thought of as a collection of points. For example, a line is just a collection of adjacent points, a circle is a collection of points that are at a certain distance from a specified point. It may be useful to think of a space as a lump of Play-Doh, with a particular moulding and separation of the Play-Doh giving a particular space.
With the Play-Doh analogy, it becomes clearer what we mean by the shape of a space. The Play-Doh may be moulded into a spherical shape, or elongated into a thin strip. Moreover, it may be broken apart into smaller balls, which collectively still make up a space, which can then also be squashed together. Algebraic topology says that spaces have the same shape when one space can be moulded into the other without breaking or glueing the space.
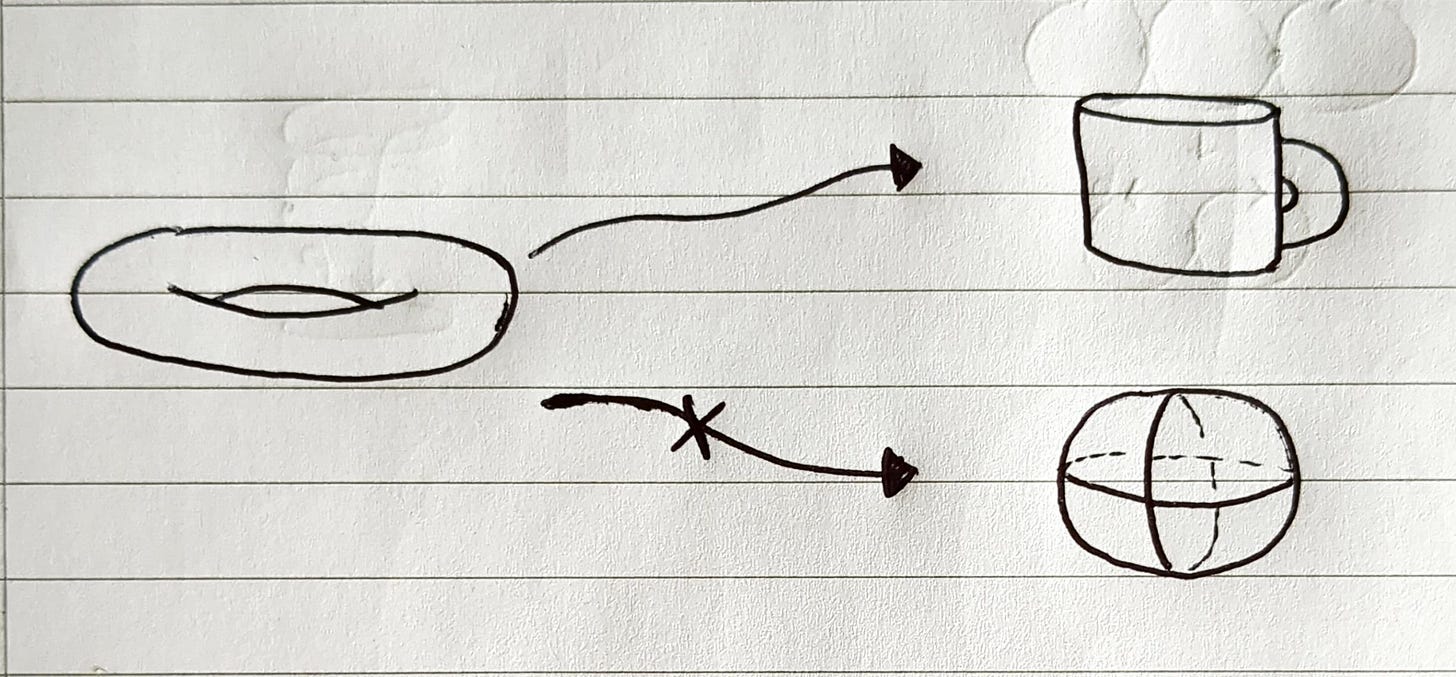
A classical example of spaces with the same shape is the doughnut and the coffee mug. Indeed, given a piece of Play-Doh in the form of a doughnut one can mould it into a coffee mug. From the everyday usage of the term shape, it may seem wrong to say that a doughnut and a coffee mug have the same shape. However, taking a global perspective we see that both spaces are just objects with a hole in them. Algebraic topology takes this more global perspective so that it can formalise the concept of shape to more complex spaces without worrying about minor details. In particular, it makes it easier to reason about the shape of spaces that do not necessarily exist in three dimensions.
Ok, so algebraic topology says that a doughnut has the same shape as a mug, but a different shape to a sphere. How is this useful? The benefit is to facilitate the formalisation of shape to enable the exploration of higher dimensional spaces where our Play-Doh analogy starts to break down.
But why do we need to know the shape of higher dimensional spaces? Suppose you are analysing a set of data points with multiple attributes. Then this point cloud of points lives in a high dimensional space. Namely, there is a dimension for each attribute of the data points. Many data analysis tasks are intrinsically connected to understanding the shape of the collection of data points. For example, clusters of data points in the high dimensional space may correspond to a subset of data points with a particular property, and thus understanding the shape of the data corresponds to performing a classification task.
Note how in the case of clusters of data points, we are not interested in the exact ordering or location of the individual points. We are just concerned with the global shape of all the points. Therefore, the algebraic topology perspective on shape seems more reasonable. Indeed, if the data points were measured differently, the exact ordering of the points may change but the global structures will remain present. Moreover, using the colloquial interpretation of shape would require the tracking of the locations of each of the individual points in the data set, which could be vast.
Although mathematical endeavours need not be motivated by practical applications, indeed the pleasure of exploring abstract mathematics should be the main source of motivation, it is clear that algebraic topology, in conjunction with being an incredibly elegant subject also has practical applications.
Loops
To extend our Play-Doh analogy to higher-dimensional and more complex spaces we use loops. More specifically, suppose you have a two-dimensional disc, such as a frisbee, and imagine placing a loop on this space with a piece of string. Without tearing the string you can deform and shrink the loop. In particular, you could contract your loop, by shortening the string, down to a small point. Doing such transformations does not change the shape of your loop.
Now take your disc and puncture a hole in it. Again suppose you have a piece of string and make a loop on your punctured disc. In this case, if your loop wrapped around the hole then you could still deform and shrink the string, however, there will be a limit to how much you can shrink the string. In particular, eventually, your loop will wrap around the hole and you will no longer be able to shrink the string without tearing it or leaving the disc. However, if your loop does not wrap around the hole, then as before you can shrink it to a point.
Therefore, we see that the disc with no hole only has only one type of loop, namely the ones that can be shrunk to a point. Whereas, the disc with a hole has two types of loop, namely the ones that can be shrunk to a point and ones that eventually wrap around the hole. We conclude that the shapes of the disc and the punctured disc are different. Indeed this is consistent with our analogy that a Play-Doh disc cannot be moulded into a Play-Doh disc with a hole without tearing the hole into the playdoh.
Algebraic topology formalises this usage of loops as a way to investigate the shape of more complicated spaces.
Loops on a Circle
Let us explore in more detail the types of loops on a punctured disc. For simplicity, we can just assume that our space is a circle of points, as one can mould a punctured disc so that it is just a circle of points. So now we are thinking of loops as wrapping around a circle. Indeed a loop must start at a point and go all the way around the circle and finish at the same point.
In particular, we make the following observation, if a loop goes around the circle twice clockwise, then It cannot be deformed into a loop that goes around the circle once clockwise without tearing it. Therefore, these loops must be different in the context of algebraic topology. Furthermore, if I have a loop that goes twice clockwise and then once anti-clockwise, this is the same as the loop that goes just once clockwise.
This suggests that we can just identify loops with a number n. If n is positive then this says the loops go around the circle n-times clockwise. If n is negative, then the loop goes around the circle n-times anti-clockwise. Moreover, we can think about adding loops together. For example, a $n$ loop and a $m$ loop combine to give a $n+m$ loop. Indeed, if have the 2 loop and adjoin the -3 loop, I get a loop that first goes two times clockwise and then three times anti-clockwise, namely the -1 loop. Therefore, the set of types of loops on a circle can be associated with the integers.
Glueing Spaces Together
Ok, so algebraic topology provides us with a tool to investigate more complex spaces, that potentially live in dimensions higher than we can visualise. However, as we cannot visualise these spaces, how are we able to define them?
Well as algebraic topology differentiates spaces by whether or not they can moulded into one another without tearing or gluing, it makes sense to construct spaces by tearing and gluing existing spaces. Indeed it is common to take relatively simple spaces, that we can investigate easily, and combine them to form more complex spaces.
For example, imagine you have a strip of paper, where one set of opposite edges is longer than the other set of opposite edges. The shape of this piece of paper is the same as that of the disc as one can imagine moulding the strip into a disc. Take this strip of paper, add a half turn to one of the short edges and then glue the short ends together.
What you are left with is called a Mobius strip, and it has the peculiar property of having only one side. Indeed, trace your finger around the strip and you'll notice that you traverse the entire strip and return to where you started.
One can go a step further and imagine glueing two Mobius strips together along this edge. Doing so gives rise to a four-dimensional space known as the Klein bottle.
In turns out that many spaces can be constructed in this way. For example, a circle is just a line that has its edges glued together. The surface of a three-dimensional sphere, like a blown-up balloon, can be thought of as a two-dimensional disk whose boundary is attached to a single point.
A doughnut can be considered taking a strip and glueing both sets of opposite edges together.
Algebraic topology formalises this process of glueing and therefore facilitates the study of high-dimensional complex spaces by extrapolating the investigations done on simpler spaces.
Understanding Neural Networks Using Topology
As previously mentioned, a set of data points can be thought of as having a shape. More specifically, the data points can be thought of as a set of samples from an underlying manifold of a high dimensional space. The shape of the manifold is likely, and so the role of the neural network is to simplify the shape of the manifold to facilitate inference [1]. With this perspective [1] attempts to demystify the black-box nature of neural networks by tracking the shape of the data throughout the network. Roughly speaking [1] looks at the different dimensional holes present in the input data as it progresses through the neural network.
Tracking the holes present in a set of data as it progresses through a network provides a quantitative insight into the inner workings of a neural network, moreover, it provides a metric to establish a neural network’s capacity to deal with data. Suppose a network is being trained for a binary classification task. If the input data has many holes of different dimensions, the data points relating to the two classes are likely intertwined in a complex way. Therefore, to perform well at the classification task, the network is incentivised to disentangle the data and eliminate these holes. Hence, as data is propagated through a well-trained network one should observe the reduction in holes present in the data.
With this insight, [1] can elucidate the underlying processes of a neural network, and understand the correlation between the architectural properties of the network to its capacity to perform a certain task. The conclusions made by [1] through these investigations are the following.
Smooth activation functions, such as the hyperbolic tangent function, have a lower capacity for simplifying the shape of input data compared to nonsmooth activation functions such as ReLU.
The majority of the shape simplification a neural network performs occurs in deeper layers. Indeed, as the layers of a neural network increase, the capacity of a neural network to disentangle input data increases.
Bibliography
[1] Naitzat, Gregory, Andrey Zhitnikov, and Lek-Heng Lim. ‘Topology of Deep Neural Networks’. arXiv, 13 April 2020. https://doi.org/10.48550/arXiv.2004.06093.