To Infinity and Beyond
Understanding Infinity
Infinity is challenging to deal with as a mathematical object and conceptually. Indeed many constructions in mathematics are just said to be ill-defined when infinity crops up. For example, dividing 10 by 2 is equivalent to saying how many times 2 goes into 10. More specifically, five 2s go into 10 so 10 divided by 2 is 5. However, what if we replaced 2 with 0? Then dividing 10 by 0 is asking how many times 0 goes into 10. Does such a number exist? Is it infinity? It cannot be some finite number like 100 or 1000000 as 0 add 0 is 0 and so repeating this how every many times will still be 0. This is an inductive argument, a type of reasoning that we will explore later. But if it were infinity that would mean that infinitely many 0s would add together to give 10, just like five 2s add together to give 10. But then if we replaced 10 with 15, by our reasoning we would also have infinitely many 0s add together to give 15. So which one is it, 10 or 15?
Introduction to Sets of Numbers
To investigate the notion of infinity further we consider sets. Sets can be thought of as just a collection of objects say
Note that the ordering of the objects in the sets is not important. That is, the set
is the same as the set
In mathematics, the most ubiquitous set is probably a set known as the natural numbers. The natural numbers contain what is colloquially known as the counting numbers, namely
So 101 is in the natural numbers, and so is 101010101.
How many objects are in the set of natural numbers? Suppose that there were only a finite number of elements in the natural numbers, then we could pick the largest one. Let us say that M is the largest number in the natural numbers. Then M+1 is another number, but as it is larger than M it cannot be in the natural numbers as we assumed M was largest. Therefore, it must be the case that there is a non-finite number of objects in the natural numbers. Is this non-finite number infinity? One may be tempted to say that the natural numbers contain an infinite number of objects, however, I will now argue why this may be problematic.
Suppose one adds all of the negative numbers to the natural numbers as well to get the set of integers
It may be intuitive to think that the integers are a larger set than the natural numbers, because after all the natural numbers are contained within the integers. However, let us try and count directly how many integers there are. To do so we are going to take an integer and perform one of the following operations.
If it is 0 label it with 0.
If it is negative we are going to label it with itself multiplied by -2.
If it is positive we are going to label it with itself multiplied by 2 and then minus 1.
For example, -3 is labelled with 6 and 7 is labelled with 13.
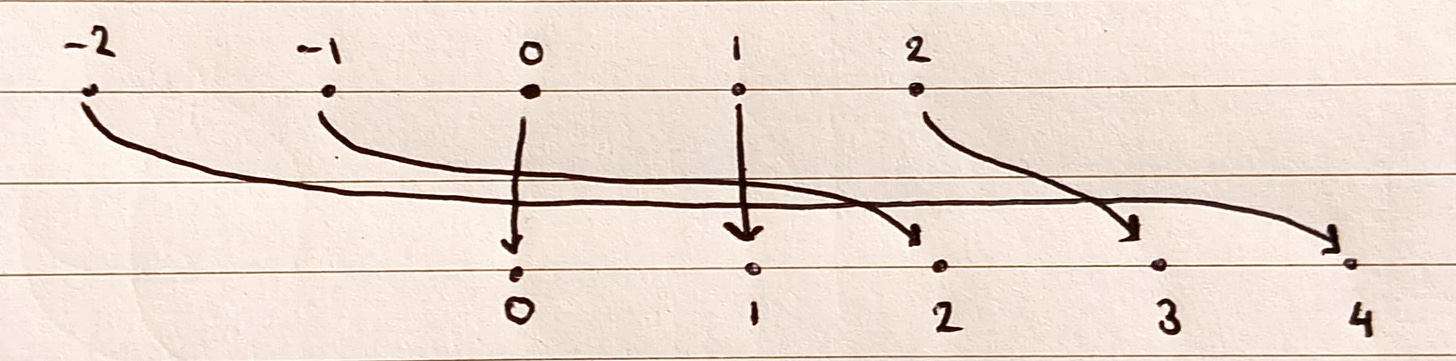
Technically, such an operation, is what is known as a bijective correspondence between the integers and the natural numbers. As for every each integer we have assigned it a unique label from the natural numbers. Moreover, every natural number labels some integer, for example, 72 is the label of -36.
As we can construct a bijective correspondence between the integers and the natural numbers, we say the natural numbers and the integers have the same number of elements. To see why this makes sense consider the finite sets. If we can construct a bijective correspondence between finite sets we are just pairing up objects from each set. We can only do this when the sets have the same number of objects.
Similarly, we can also show that
is equal in size to the natural numbers. We can also show that the set of rational numbers, that is the set of fractions, is equal in size to the natural numbers. More generally, we say that any set that is equal in size to the natural numbers is countably infinite.
Now you are probably wondering if there are any sets that we would consider to be infinite in size, but are not equal in size to the natural numbers. Of course, the answer to this is yes otherwise I would not have said countably infinite, and I would have just said that natural numbers have infinitely many elements. Indeed the set of real numbers is not the same size as the set of natural numbers. The set of real numbers contains all numbers such as fractions, decimals, counting numbers, and negative numbers...(apart from complex numbers). So for example, 0.28394328... is a real number, -1 is a real number, π is a real number and so on. Now as the natural numbers are contained in the real numbers, intuitively, there are more real numbers than natural, however, we saw that this intuition can deceive. More formally, one can show that no bijective correspondence exists between the natural numbers and the real numbers. Instead, one can only construct an injective correspondence. That is, a correspondence where every natural number can be used as a unique label for a real number, however, we are not able to label all the real numbers. Therefore, we deduce that the real numbers are a strictly larger set than the natural numbers. In particular, we say that the real numbers are uncountably infinite.
I will stop the discussion of numbers here before opening a can of worms. Indeed from this discussion, there remain many open questions.
Is countably infinite the smallest infinity?
Is there are level of infinity between countable and uncountable?
Are there levels of infinity beyond uncountable?
What sets of numbers are equal in size to the real numbers?
For the curious, I refer you to the study of aleph numbers.
Induction
Although an elusive concept, infinity can be leveraged to construct rigorous mathematical proofs. Mathematical induction is a method of reasoning that capitalises on the successive and discrete nature of the countably infinite. I have already identified some instances where I have used an inductive argument. In a more general setting, inductive argument aims to determine whether a particular property is held by a set of countably many objects. We must be only dealing with countably many objects as this means that we can order them and consider each element of the set in turn. Inductive reasoning does not work for uncountably many objects.
To sketch the inductive argument we will assume that we want to show a property of the natural numbers. After all any countable set can be exactly relabelled with the natural numbers. Suppose that we want to show that every natural number has the property PROP, then the inductive argument proceeds as follows.
Check that 0 has PROP.
As that and arbitrary natural number k has PROP.
Using the fact that k has PROP, show that k+1 has PROP.
Completing each of these steps will then allow you to conclude that all natural numbers have PROP. To see why this conclusion follows let us consider a concrete example. Suppose that we want to show that the sum of the first n natural numbers is equal to
For 0 it is clear that the formula equals the sum of the first 0 natural numbers.
Assume that the sum of the first k natural numbers is
\(\frac{1}{2}k(k+1).\)The sum of the first k+1 numbers is just the sum of the first k plus k+1. We know what the sum of the first k is, and so the sum of the first k+1 is
\(\frac{1}{2}k(k+1)+k+1=\frac{1}{2}(k+1)(k+2).\)Therefore, k also satisfies the property and so the mathematical induction is complete.
The basic idea behind mathematical induction is akin toppling dominos. More specifically, we can think of the natural numbers as dominos, and we suppose that a domino topples if it has the property. Checking that the property holds for (k+1)-th domino assuming it holds for k-th is just making sure that if the k-th domino topples then the (k+1)-th will be knocked and toppled. Having checked this, it is then sufficient to check that some domino has the property as this means it will topple and trigger all subsequent dominos to topple. More specifically, we check that 0 has the property. Once this is done we know then that the 1-st domino to topple, which will then cause the 2-nd to topple and so on. Therefore, all the dominos will eventually fall and we can conclude that the property holds for all natural numbers.
Limits
Suppose you are running one hundred metres down the straight of a running track, you can see the finish line in the distance. To reach that finish you must run the first half of the race. After that, you still have fifty metres to go. Again it is clear that you must run half of this distance before you can reach the finishing line. After you have done that you are left with twenty-five metres to go and, as before, you note that you have to run half of the remaining distance before reaching the finishing line. After you have done this you have twelve and a half metres to go. Again you realise that you must run the next half before finishing, but now you start getting concerned. Each time you run half the remaining distance there is still an equal half left to run. Therefore, no matter have much you run you will still have a little to go, will you ever reach the finish line? Fortunately, the answer is yes, and the reason is to do with something called geometric series.
A geometric sequence of numbers is a sequence of numbers where the next number in the sequence is some constant multiple of the previous. For example,
is a geometric sequence as the next number in the sequence is given by twice the previous. Similarly,
is a geometric sequence as the next number in the sequence is a third of the previous. For the first of these geometric sequences, the numbers in the sequence continue to get larger, and for the second of these geometric sequences, the numbers in the sequence get closer to zero.
With sequences, it is interesting to ask whether adding the elements of the sequence will result in a finite number. This may seem not possible at first as you are adding infinitely many numbers together and so surely their sum should be a non-finite number. However, it turns out that if the numbers in the sequence get sufficiently small sufficiently fast, then their sum will be finite. However, the numbers in a sequence getting small is not a sufficient condition for the corresponding sum to be finite. For example, the sum
does not give a finite number. However,
does give a finite number. In fact,
For a geometric series where the terms of the sequence get smaller, the sum of all the elements of the sequence is guaranteed to be finite. In particular, the sum of the geometric sequence
is 1. So even though you need to reach infinitely many milestones to complete your hundred-metre race, the cumulation of all those milestones is just one big finite milestone which you can complete.